Beiträge von TBM

Ja genau, ich habe mit Akabak simuliert.

Eine gute Anleitung ist mir da nicht bekannt. Ich habe mir die Beispiele angesehen und zum Teil nachgebaut und alle Komponenten nachvollzogen sowie in die Hilfe geschaut.

Hier die Simualtion eines rechteckigen Horns in unendlicher Schallwand mit den beiden zuletzt simulierten Konturen des doppelten konischen Waveguides:

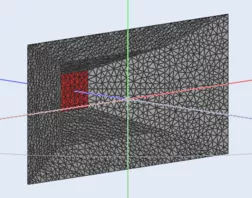
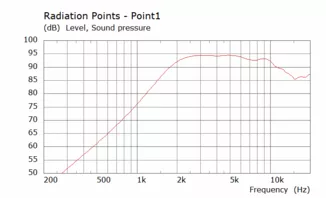
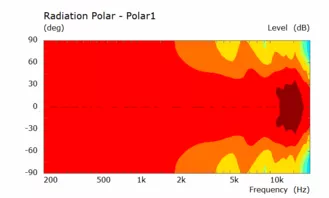
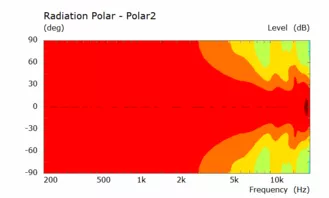
Es zeigt sich ein relativ gleichmäßiger Frequenzgang, der aber noch einen breitbandigen Einbruch über 10 kHz enthält und eine relativ gleichmäßige horizontale und vertikale Abstrahlung wobei die horizontale deutlich breiter ist als die vertikale.

Dieser Kontur dient als Startpunkt für weitere Simulationen mit an die Kalotte angepasstem Hornmund und einer endlichen Schallwand.

Hinweis: Im nachfolgenden werden die sowohl die begriffe Horn als auch Waveguide für das gleiche Bauteil verwendet, da dieses Waveguide von der Geometrie nichts anderes ist als ein Horn. Waveguide beschreibt hier eher die Funktion und Horn die Physik dahinter.

Da dies mein erster Waveguide ist, den ich auslege, zunächst ein paar Grundlegende Simulation um die zusammenhänge zu verstehen. Aus Gründen der Simulationszeit erstmal ein paar achsensymmetrische Simulationen.

Zunächst einmal ein konisches Waveguide variabler Länge und Durchmesser in unendlicher Schallwand:

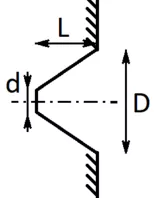
Schauen wir uns den Frequenzgang auf Achse und das Abstrahlverhalten in Abhängigkeit von der Länge L und dem Munddurchmesser D an. Der Halsduchmesser sei d = 20 mm.

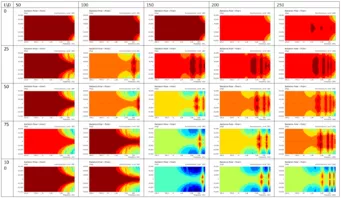
Es zeigt sich, dass die Ergebnisse bei Hornlänge 0 bis auf kleinere numerische Ungenauigkeiten identisch sind. Dies war auch zu erwarten, da das Waveguide hier einfach nur einen Teil der unendlichen Schallwand darstellt. Bei sehr großem Öffnungswinkel (z.B. L = 25 mm, D = 250 mm) ist die Abstrahlung sehr breit und der Schalldruckgewinn nahezu nicht vorhanden. Bei geringen Öfnungswinkel (z.B. L = 100mm, D = 100mm) ist die Abstrahlung sehr eng. Bei den meisten Abmessungen treten leichte bis starke Auslöschungen und Überhöhungen auf.

Um die Abhängigkeit des Bündelungsverhaltens von Länge und Durchmesser besser beurteilen zu können wird die Bündelung nachfolgend durch jeweils zwei Zahlenwerte ausgedrückt. Zum einen die Frequenz ab der der 60°-Frequenzgang gegenüber dem Axialfrequenzgang (0°) um 6 dB abgefallen ist und zum anderen der Winkel ab dem der Schalldruck gegenüber 0° um 6 dB abgefallen ist.

-6dB bei 60°:

Abstrahlwinkel bei 4 kHz:

Es zeigt sich recht deutlich, dass die Frequenz ab der Bündelung auftritt in erster Linie nur vom Mundurchmesser abhängt. Dir stärker der Bündelung steigt mit steigender Hornlänge und damit sinkendem Öffnungswinkel.

Zu dem 7-Zoll Arcosia scheint von diesen Werten das 150x50-Waveguide recht gut zu passen, daher wird dieses erstmal für weitere Untersuchung betrachtet.

Das konische 150x50-Waveguide hat auf Achse zwei unschöne Auslöschungen bei ca. 9 kHz und ca. 18 kHz. Um die passende Bündelung zu Erhalten aber keine zu großen Auslöschungen und Überhöhungen wird ein weiterer Freiheitsgrad hinzugefügt: Ein zweistufiges konisches Horn. Hier können wir unterschiedliche Öffnungswinkel am Hornhals und am Hornmund wählen um zum einen eine passende Bündelung zu erhalten aber zum anderen einen geringeren Impedanzsprung am Hornmund zu erhalten womit die Reflektionen und damit die Erhöhungen und Auslöschungen reduziert werden.

Die Parameter dieser Geometrie Lauten wie folgt:

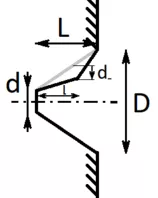
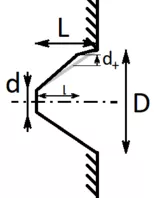
Prozentuale Länge der ersten Stufe

p_L = l/L

Prozentuale Verschiebung des Zwischenpunktes in Radialer Richtung

p_D = { 2*d-/(d(x=L)-d) für p_D<0 ; 2*d+/(D-d(x=L)) für p_D>0 }

Also

p_D = 0: konisches Horn

p_D = -100%: erste Stufe zylinderförmig

p_D = 100%: zweite Stufe zylinderförmig

Schauen wir uns jetzt mal den Frequenzgang und das Abstrahlverhalten für unterschiedliche Werte für p_D und p_L für das 150mmx50mm Horn an:

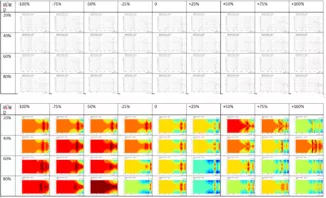
Bei positivem p_D (also Öffnungswinkel am Hals größer als am Mund) ergeben sich sehr viele und teils sehr starke Auslöschungen und Überhöhungen und ein extrem ungleichmäßiges Abstrahlverhalten. Bei negativem p_D (also Öffnungswinkel am Hals kleiner als am Mund) sieht es erwartungsgemäß besser aus.

Die gleichmäßigste Abtrahlung ergibt sich, wenn der zwischenpunkt eher Richtung Hornmund gerichtet ist bei p_L im Bereich 60-80% und bei moderater Verschiebung nach innen bei p_L im Bereich -25% bis -50%.

Ein sehr glatter Frequenzgang ergibt sich z.B. bei p_L = 80% und p_D = -50%, aber hier wird die Bündelung zu hohen Frequenzen etwas sehr stark, was zu einer Verfärbung außerhalb der Achse führt. Ein anderes mögliches Extrem wäre ein CD(Constant Directivity)-Horn. Hier ist die Bündelung oberhalb einer gewissen Frequenz konstant. Dies ist auch nicht ganz das was ich möchte, da hier außerhalb der Achse einfach nur der gesamte Hochtöner leiser wird aber der Tieftöner nicht. Im nachfolgenden wird also eine leicht zunehmende Bündelung angestrebt. Was hier "leicht zunehmend" heißt, kann ich nicht quantifizieren und wird im nachfolgenden nach Gefühl beurteilt.

Ein bisschen Rumprobieren ergab die Werte p_L = 70% und p_D = -35%:

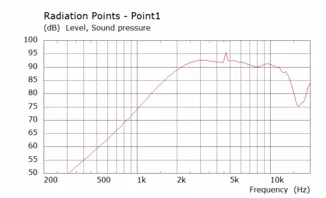
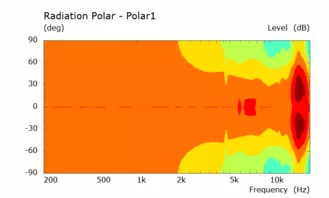
Bis auf den Einbruch bei knapp über 15 kHz sieht das ganze doch schonmal gut aus (Dieser Bereich wird ohnehin durch die Ankoppelung der Kalotte an den Hornhals noch stark beeinflusst und daher erstmal nicht weiter betrachtet). Bei halbiertem Durchmesser (vertikal soll der Waveguide schmaler sein und damit enger abstrahlen um Boden- und Deckenreflektionen zu verringern) sieht das folgendermaßen aus:

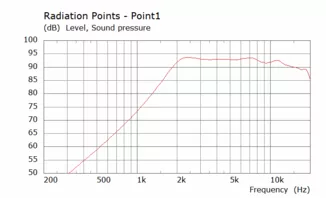
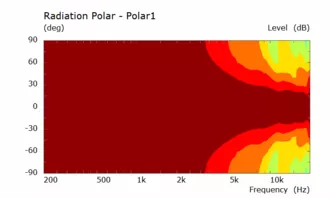
Ein schön gleichmäßiger Frequenzgang und eine engere leicht zunehmende Bündelung. Diese beiden Konturen eignen sich für eine Simulation eines rechteckigen Horns. Diese aber erst im nächsten Post, da ich sonst die Grenze an Dateianhängen überschreite.

Hallo zusammen,

hier möchte ich die Entwicklung der Lautsprecher für mein Wohnzimmer dokumentieren.

Bisher hat keiner meiner Lautsprecher einen Namen erhalten, aber da ich die Entwicklung diesmal in Form eines Threads dokumentiere, hielt ich einen Namen für angebracht. Da ich was solche Dinge angeht nicht sonderlich kreativ bin habe ich als Benennung einen Code gewählt, wie es z.B. auch Genelec macht. Der Code ist folgendermaßen aufgebaut:

XXYZZA

XX: zweistellige Buchstabenkombination die die Art des Lautsprechers beschreibt (WG = Waveguide, DW = Doppelwaveguide, HN = Horn, DH = Doppelhorn, SW = Subwoofer etc. Für "normale" Lautsprecher ist mir noch keine Buchstabenkombination eingefallen)

Y: Anzahl der Wege

ZZ: Größe des Tieftöners in Zoll (Zweistellig)

A: Fortlaufende Nummer, falls mehrere Lautsprecher in die gleiche Kategorie fallen

Bei dieser Entwicklung handelt es sich also um einen Lautsprecher mit einem Waveguide, mit 2 Wegen und einem 7-Zoll Tieftöner.

Entwurf

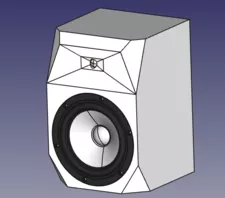
Die Idee ist einen 7 Zoll-Tieftöner mit einem 19 mm-Hochtöner zu verheiraten. Zur Anpassung des Abstrahlverhaltens dient ein Waveguide.

Da ich nicht über eine (CNC-)Fräsmaschine verfüge und mir das kantige Design irgendwie gefällt soll der Waveguide so gestaltet werden, dass ich die einzelnen Segmente mit einer Kappsäge gefertigt kriege und diese dann zusammensetze. Da ich dem Waveguide keine unendliche Schallwand spendieren kann und will, sollen zur Minimierung der Kantenreflektionen breite Fasen verwendet werden.

Chassisauswahl

Hochtöner:
19 mm Magnesiumkalotte aus dem ausfahrbaren Hochtöner des B&O-Systems im BMW.

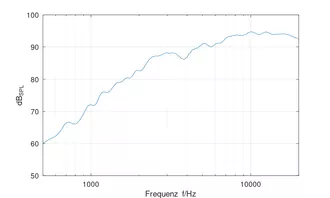
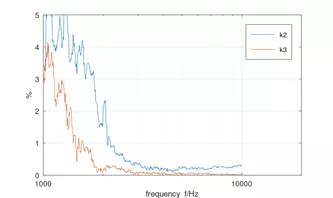
links: SPL bei 1W/1m bei freier Aufhängung in einem reflektionsarmen Messraum.

rechts: Zugehörige 2. und 3. Harmonische bei einem 1W-Sinussignal

Es zeigen sich durch die kleine steife und leichte Membran bis 20 kHz keine erkennbaren Resonanzen.

Oberhalb von 2 kHz sind beide Klirr-Komponenten unterhalb von 1%. Oberhalb von 3 kHz sogar unter 0,5%.

Tieftöner:

7 Zoll Magnesium-Composite-Konus Eton Arcosia 7-218

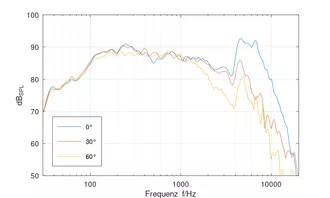
links: SPL bei 1W/1m in 700 Liter in 940 mm x 1240 mm-Schallwand in einem reflektionsarmen Messraum.

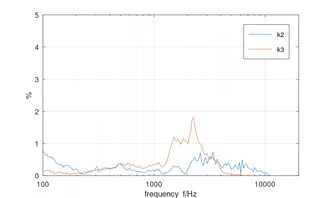
mitte: Zugehörige 2. und 3. Harmonische bei einem 1W-Sinussignal

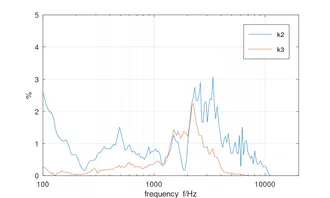
rechts: Zugehörige 2. und 3. Harmonische bei einem 10W-Sinussignal

Es zeigt sich eine - für Metallmembranen typisch - ausgeprägte Resonanz bei 5-6 kHz. Demzufolge zeigt der k2 bei der halben Frequenz und der k3 bei einem drittel der Frequenz eine stärkere Ausprägung. Allerding halten sich diese selbst bei 10W noch in Grenzen.

Bei knapp über 1 kHz fängt das Chassis an zu bündeln. Bei rund 2,5 kHz ist die Abstrahlung bei 60° um etwa 6 dB gegenüber 0° gesunken, bei ca. 4 kHz entsprechend die 30°-Abstrahlung. Diese beiden Punkte dürften gut als klar definierbare Punkte zur Auslegung Waveguides dienen, da irgendwo dazwischen auch die Grenzfrequenz liegen sollte um zum einen keine Probleme mit der Resonanz des Tieftöners und keine zu hohen Auslenkungen des kleinen Hochtöners zu bekommen.

Zur Zeit bin ich gerade an ein paar Grundlegenden Simulationen eines Waveguides um ein bisschen ein Gefühl der Zusammenhänge zu bekommen, da dies mein erstes Waveguide ist, dass ich auslege. Sobald ich diesbezüglich etwas vorzeigbares habe werde ich es hier präsentieren.

Ich bin für Anregungen offen. Gerne auch Hinweise was ich evtl. beachten und was ich unbedingt vermeiden sollte.

Hast du auch eine Impedanzmessung im unverbauten Zustand gemacht? Treten dort die Buckel nicht auf?

Ich würde die Resonanzen erstmal mit akustischen Messungen überprüfen. Am besten noch mit einer Nahfeldmessung vorm Chassis und eine vorm Port. Wenn möglich auch noch welche im Port in verschiedenen Tiefen (Das Mikro verschieden tief in den Port reinschieben). Dann solltest du ein klares Bild bekommen ob es sich bei einer Resonanz um eine Portresonanz handelt.

Hast du vllt. noch die inneren Abmessungen? Dann kann man nachrechnen ob eine der Resonanzen einer Raummode im Gehäuse entspricht.

Das sieht handwerklich schon mal sehr gut aus.

Du hast aber eine sehr wichtige Information vergessen: Was wird das überhaupt, wenn es fertig ist

Zitat von ChrissN

Metrische Schrauben brauchen keinen Druck beim anziehen, was die Gefahr des Abrutschens verringert.

Es sei denn sie haben einen Philipps (PH) Kreuzschlitzkopf. Hier muss nämlich eine axiale Kraft aufgebracht werden um ein Drehmoment zu übertragen. Allerdings ist diese geringer als typischerweise bei Holzschrauben.

Y-Kings Worte waren noch einfacher

Ich kann mir nicht vorstellen, dass die Impedanzkorrektur bei einem Transistorverstärker schadet. Sie ist halt dort nur nicht nötig.

Bei einem Röhrenverstärker ist u.a. durch die Ausgangssübertrager keine hohe Gegenkopplung möglich. Damit hat der Röhrenverstärker effektiv eine hohe Ausgangsimpedanz.

Jetzt fangen die einfachen Worte an: Die hohe Ausgangsimpedanz ist so als würdest du einen Widerstand in Reihe mit dem Lautsprecher schalten. Damit hast du einen Spannungsteiler.

Wenn die Impedanz des Lautsprechers über die Frequenz konstant wäre, wäre alles gut. Wenn der Lautsprecher jetzt bei einer Frequenz eine Impedanzspitze hat liegt an dem Lautsprecher eine höhere Spannung an als bei den anderen Frequenzen. Damit ergibt sich ein ungleichmäßiger Frequenzgang.

Um das zu reduzieren setzt man eine Impedanzkorrektur ein. Diese bewirkt eine gleichmäßigere Impedanz, was den Frequenzgang an einem Röhrenverstärker begradigt.

Gute Idee mit den Schnellbauschrauben.

Durch meine Badezimmerrenovierung habe ich zum Glück noch einige davon

Die CNC-Fräse fehlt mir auch. Da mir der 3D-Drucker ebenfalls fehlt , denke ich an einen eckigen Waveguide mit geraden Flanken. evtl. in 2 Segmenten.

Etwas in dieser Form nur flacher:

Eine gute Anleitung zu Akabak kenne ich jetzt nicht. Da ich mich mit der Randelementmethode (BEM) im allgemeinen auskenne, reichte es zumindest mir mir die Beispiele anzusehen und diese nachzuvollziehen und gründlich in die Hilfe reinzulesen..

Ich würde empfehlen mir zumindest erstmal folgende Beispiele anzusehen:

• BEM > 2D > Cone IB (2D). Hier kann es auch helfen das Modell in einer leeren Datei nachzubauen und alle Komponenten versuchen nachzuvollziehen. Als Hinweis: Das Interface ist wichtig, da im Bereich des Lautsprechers (Subdomain "Cone") keine unendliche Schallwand vorhanden ist (ausgeschnitten) und sonst (vereinfacht gesagt) eine Reflektion an dem Bereich der unendlichen Schallwand miteingerechnet wird, der gar nicht existiert. Dann würde natürlich Unsinn herauskommen.
• BEM > 2D > Horn 2D. sieht auch interessant aus. Hier ist vor allem das Prinzip mit den Subdomains und Interfaces sehr gut ersichtlich. Hierfür hilft es das grundlegende Prinzip der Interfaces und Subdomains verstanden zu haben. Ich empfehle dazu folgenden Artikel: http://www.randteam.de/Publications/P…Subdomains.html
• BEM > Loudspeakers > Speaker Cabinet SP38..... Das sind mehrere Simulationsmodelle des gleichen Lautsprechers aber mit unterschiedlichen herangehensweisen, Diese Beispiele zeigen sehr gut die Verschiedenen Elemente, die Akabak mitbringt.
• BEM > Loudspeakers > 45Tower - BEM... Diese beiden Beispiele dürften auch noch interessant sein, da es deinem Problem recht nahe kommt

Ich kenne mich ein wenig in Akabak aus.

Ich plane sogar etwas ähnliches in naher Zukunft. Nur vermutlich aus Holz und nicht 3D-gedruckt.

Was denn für einen Online-Kurs?

Ja, ich habe mal Messungen des Room-Gains gemacht um ihn mit der Theorie zu vergleichen.

Allerdings nur in einem Auto, aber das sollte sich auf einen geschlossenen Wohnraum übertragen lassen.

Ich habe dafür einen 165mm Lautsprecher in einem flachen Gehäuse einmal im Freien in 1m Abstand gemessen. Das Gehäuse lag dabei flach auf dem Boden. Für den Bassbereich hatten wir damit annähernd Halbraumbedingungen. Das womit beispielsweise auch WinISD simuliert.

Dann habe ich den Lautsprecher einmal in meinem Auto (Hyundai i30 Kombi) und einmal in dem meiner Frau (Kia Soul) in den Kofferraum gelegt und gemittelt über 4 Sitze und beim Fahrersitz in zwei verschiedenen Höhen (Brust und Ohrhöhe) gemessen.

Hier das Ergebnis:

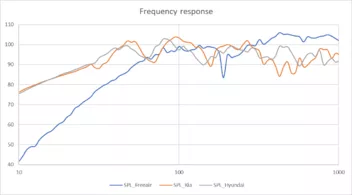
Dann habe ich die Differenz mit der Theorie verglichen:

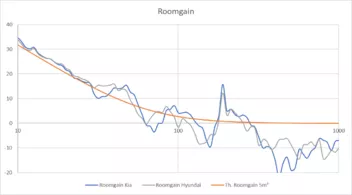
Folgendes theoretisches Modell habe ich dabei angenommen:

Der Schalldruck im Raum ist die Summe aus zwei Komponenten:

• "normaler" Schalldruck der durch die Strahlungsimpedanz auf der Membran entsteht und proportional zur Beschleunigung der Membran ist
• Druckänderung im Raum durch komprimierung der Luft durch die Auslenkung der Membran (Druckänderung proportional zu Volumenänderung), welcher proportional zur Auslenkung ist.

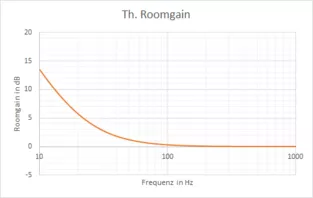
Die zweite Komponente ist dabei abhängig von dem Raumvolumen. Für einen einen typischen 20 m² Raum mit 2,5 m Deckenhöhe also 50 m³ Raumvolumen sähe der Roomgain folgendermaßen aus

Ich habe mal eine Loop-Back Messung meiner USB-Soundkarte (TerraTec Aureon 5.1 USB MKII) und eine Messung des Ausgang der Internen Soundkarte meinen Arbeits-Laptops durchgeführt (Als Eingang habe ich den Line-In meiner USB-Soundkarte verwendet).

Hier einmal die TerraTec:

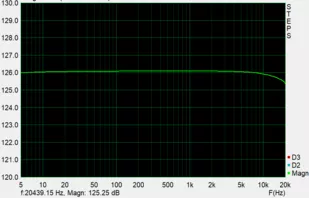
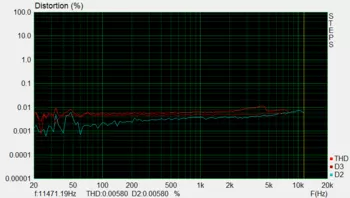
Hier die Onboard-Soundkarte

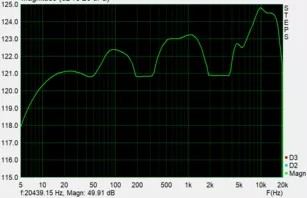
Anscheinend läuft hier ein Klangprogramm, das durch einen verbogenen Frequenzgang und dem Hinzufügen einiger harmonischer ein "dynamischeres" Klangbild hervorrufen soll. Es lässt sich zwischen 3 verschiedenen Klangprogrammen (in der Software als "Hörerlebnis" bezeichnet) wählen: Musik (standardmäßig ausgewählt), Film und Stimme. Irgendein Neutrales gibt es nicht, die anderen beiden waren sogar noch schlimmer als das eingestellte..

Der zusätzliche Equalizer ist auf neutral eingestellt.

Zum Messen ist das völlig ungeeignet. Für Impedanzmessungen mag das aber noch gehen.

Für Bestimmungen der [definition='1','0'] TSP "> TSP [/definition] kann so ein Hochpass, der bei dieser Soundkarte zwar noch recht schwach, aber bei anderen Onboard-Soundkarten stärker ausgeprägt sein kann, schon zu einem Problem werden:

• Die AD-Wandler haben 16 Bit (Ich denke, das dürfte auf Onboard-Soundkarten zutreffen)
• Wir Messen in der Regel nicht mit 0dBFS (Zum einen, weil dann Nichtlinearitäten das Ergebnis verfälschen können und weil der Soundkartenausgang wahrscheinlich auch nicht genügend Strom liefern kann) Damit gehen schon ein paar Bit verloren. Sagen wir 2-3 Bit.
• Jetzt haben wir vor dem Messobjekt einen 100 Ohm Widerstand (Oder einen anderen in ähnlicher Größenordnung) und unser Messobjekt kann ein Lautsprecher mit 4 oder gar 2 Ohm Nennimpedanz sein. Im Impedanzminimum verlieren wir damit nochmal 5 bis 6 Bit also bleiben uns noch ca. 7 bis 8 Bit übrig. Das genügt für eine Genauigkeit von rund 1%.
• Letzteres gilt aber nur, wenn die Soundkarte einen linearen Frequenzgang hat. Wenn wir jetzt einen Lautsprecher mit einer sehr tiefen Resonanzfreuquenz messen wollen, interessiert uns auch die Impedanz bei 10 Hz oder gar tiefer. Wenn wir jetzt einen Hochpass haben, der etwas höher als bei der obigen Soundkarte liegt, können wir bei den 10 Hz schon mal einen Abfall von 10 dB oder mehr haben. Damit verlieren wir nochmals 2 Bit oder so und uns bleiben im schlimmsten Fall nur noch 5 Bit oder weniger übrig. Das ergibt eine Auflösung von nur noch 3% oder schlechter.

Das kann also schon mal sehr ungenaue Messungen ergeben.

Weiterer Vorteil: Wenn man irgendeinen Fehler beim Verkabeln macht, ist im Zweifelsfall nur die USB-Soundkarte defekt, die sich erheblich einfacher ersetzen lässt als die Interne des Computers.

Wenn es günstig sein soll, kann ich die Behringer U-Control UCA202 empfehlen.

Messtechnisch besser ist noch die TerraTec Aureon 5.1 USB MKII, allerdings wird die schon lange nicht mehr verkauft.

Von Messergebnisse verfälschen kann man nicht sprechen. Durch die eingebaute Soundkarte hast du sogar den Vorteil, dass die Messungen unabhängig vom verwendeten Computer sind. Insbesondere wenn du an einem Laptop misst, denn die internen Soundkarten sind teilweise sehr schlecht.